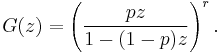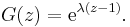Probability-generating function
In probability theory, the probability-generating function of a discrete random variable is a power series representation (the generating function) of the probability mass function of the random variable. Probability-generating functions are often employed for their succinct description of the sequence of probabilities Pr(X = i) in the probability mass function for a random variable X, and to make available the well-developed theory of power series with non-negative coefficients.
Contents |
Definition
Univariate case
If X is a discrete random variable taking values in the non-negative integers {0,1, ...}, then the probability-generating function of X is defined as [1]
where p is the probability mass function of X. Note that the subscripted notations GX and pX are often used to emphasize that these pertain to a particular random variable X, and to its distribution. The power series converges absolutely at least for all complex numbers z with |z| ≤ 1; in many examples the radius of convergence is larger.
Multivariate case
If X = (X1,...,Xd ) is a discrete random variable taking values in the d-dimensional non-negative integer lattice {0,1, ...}d, then the probability-generating function of X is defined as
where p is the probability mass function of X. The power series converges absolutely at least for all complex vectors z = (z1,...,zd ) ∈ ℂd with max{|z1|,...,|zd |} ≤ 1.
Properties
Power series
Probability-generating functions obey all the rules of power series with non-negative coefficients. In particular, G(1−) = 1, where G(1−) = limz→1G(z) from below, since the probabilities must sum to one. So the radius of convergence of any probability-generating function must be at least 1, by Abel's theorem for power series with non-negative coefficients.
Probabilities and expectations
The following properties allow the derivation of various basic quantities related to X:
1. The probability mass function of X is recovered by taking derivatives of G
2. It follows from Property 1 that if random variables X and Y have probability generating functions that are equal, GX = GY, then pX = pY. That is, if X and Y have identical probability-generating functions, then they have identical distributions.
3. The normalization of the probability density function can be expressed in terms of the generating function by
The expectation of X is given by
More generally, the kth factorial moment, E(X(X − 1) ... (X − k + 1)), of X is given by
So the variance of X is given by
4.GX(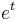 ) = MX(t) where X is a random variable, G(t) is the probability generating function and M(t) is the moment-generating function.
) = MX(t) where X is a random variable, G(t) is the probability generating function and M(t) is the moment-generating function.
Functions of independent random variables
Probability-generating functions are particularly useful for dealing with functions of independent random variables. For example:
- If X1, X2, ..., Xn is a sequence of independent (and not necessarily identically distributed) random variables, and
- where the ai are constants, then the probability-generating function is given by
- For example, if
- then the probability-generating function, GSn(z), is given by
- It also follows that the probability-generating function of the difference of two independent random variables S = X1 − X2 is
- Suppose that N is also an independent, discrete random variable taking values on the non-negative integers, with probability-generating function GN. If the X1, X2, ..., XN are independent and identically distributed with common probability-generating function GX, then
- This can be seen, using the law of total expectation, as follows:
- This last fact is useful in the study of Galton–Watson processes.
- Suppose again that N is also an independent, discrete random variable taking values on the non-negative integers, with probability-generating function GN and probability density
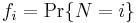 . If the X1, X2, ..., XN are independent, but not identically distributed random variables, where
. If the X1, X2, ..., XN are independent, but not identically distributed random variables, where 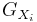 denotes the probability generating function of
denotes the probability generating function of 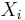 , then
, then
- For identically distributed Xi this simplifies to the identity stated before. The general case is sometimes useful to obtain a decomposition of SN by means of generating functions.
Examples
- The probability-generating function of a constant random variable, i.e. one with Pr(X = c) = 1, is
- The probability-generating function of a binomial random variable, the number of successes in n trials, with probability p of success in each trial, is
- Note that this is the n-fold product of the probability-generating function of a Bernoulli random variable with parameter p.
- The probability-generating function of a negative binomial random variable, the number of failures occurring before the rth success with probability of success in each trial p, is
- Note that this is the r-fold product of the probability generating function of a geometric random variable.
- The probability-generating function of a Poisson random variable with rate parameter λ is
Related concepts
The probability-generating function is an example of a generating function of a sequence: see also formal power series. It is occasionally called the z-transform of the probability mass function.
Other generating functions of random variables include the moment-generating function, the characteristic function and the cumulant generating function.
|
|||||||||||||
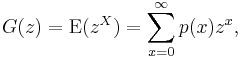
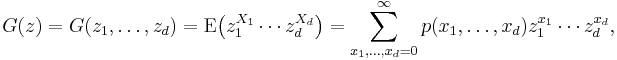
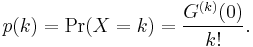
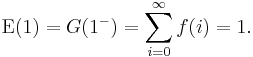
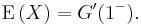
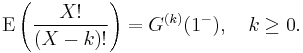
![\operatorname{Var}(X)=G''(1^-) %2B G'(1^-) - \left [G'(1^-)\right ]^2.](/2012-wikipedia_en_all_nopic_01_2012/I/587e59467fbf787a71f5c6479ca4471d.png)
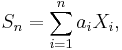
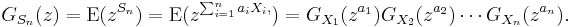
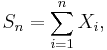
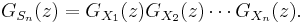
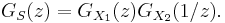
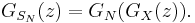
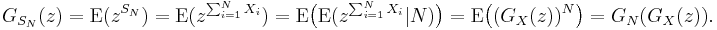
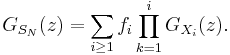

![G(z) = \left[(1-p) %2B pz\right]^n.](/2012-wikipedia_en_all_nopic_01_2012/I/7bfa524b99f1a030664f99077deb54b4.png)